thursday,25 Juli 2019

Distribusi Frekuensi

Definisi: Distribusi Frekuensi adalah daftar nilai data (bisa nilai individual atau nilai data yang sudah dikelompokkan ke dalam selang interval tertentu) yang disertai dengan nilai frekuensi yang sesuai.

Hasil pengukuran yang kita peroleh disebut dengan data mentah. Besarnya hasil pengukuran yang kita peroleh biasanya bervariasi. Apabila kita perhatikan data mentah tersebut, sangatlah sulit bagi kita untuk menarik kesimpulan yang berarti. Data mentah tersebut perlu di olah terlebih dahulu sehingga kita bisa memperoleh gambaran yang baik mengenai data tersebut.

Pada bahasan kali ini, smartstat akan menguraikan mengenai pengertian distribusi frekuensi yang disertai dengan contoh dan Teknik Pembuatan Tabel Distribusi Frekuensi. Selain itu, akan dibahas juga mengenai Distribusi Frekuensi Relatif dan Distribusi Frekuensi kumulatif, Histogram, Poligon Frekuensi, dan Ogive.

Pada saat kita dihadapkan pada sekumpulan data yang banyak, seringkali membantu untuk mengatur dan merangkum data tersebut dengan membuat tabel yang berisi daftar nilai data yang mungkin berbeda (baik secara individu atau berdasarkan pengelompokkan) bersama dengan frekuensi yang sesuai, yang mewakili berapa kali nilai-nilai tersebut terjadi. Daftar sebaran nilai data tersebut dinamakan dengan Daftar Frekuensi atau Sebaran Frekuensi (Distribusi Frekuensi).

Dengan demikian, distribusi frekuensi adalah daftar nilai data (bisa nilai individual atau nilai data yang sudah dikelompokkan ke dalam selang interval tertentu) yang disertai dengan nilai frekuensi yang sesuai.

Pengelompokkan data ke dalam beberapa kelas dimaksudkan agar ciri-ciri penting data tersebut dapat segera terlihat. Distribusi frekuensi ini akan memberikan gambaran yang khas tentang bagaimana keragaman data. Sifat keragaman data sangat penting untuk diketahui, karena dalam pengujian-pengujian statistik selanjutnya kita harus selalu memperhatikan sifat dari keragaman data. Tanpa memperhatikan sifat keragaman data, penarikan suatu kesimpulan pada umumnya tidaklah sah.

Sebagai contoh, perhatikan contoh data pada Tabel 1. Tabel tersebut adalah daftar nilai ujian Matakuliah Statistik dari 80 Mahasiswa (Sudjana, 19xx).

Tabel 1. Daftar Nilai Ujian Matakuliah Statistik



Sangatlah sulit untuk menarik suatu kesimpulan dari daftar data tersebut. Secara sepintas, kita belum bisa menentukan berapa nilai ujian terkecil atau terbesar. Demikian pula, kita belum bisa mengetahui dengan tepat, berapa nilai ujian yang paling banyak atau berapa banyak mahasiswa yang mendapatkan nilai tertentu. Dengan demikian, kita harus mengolah data tersebut terlebih dulu agar dapat memberikan gambaran atau keterangan yang lebih baik.

Bandingkan dengan tabel yang sudah disusun dalam bentuk daftar/distribusi frekuensi (Tabel 2a dan Tabel 2b). Tabel 2a merupakan distribusi frekuensi dari data tunggal dan Tabel 2b merupakan daftar frekuensi yang disusun dari data yang sudah di kelompokkan pada kelas yang sesuai dengan selangnya. Kita bisa memperoleh beberapa informasi atau karakteristik dari data nilai ujian mahasiswa.

Tabel 2a.



Pada Tabel 2a, kita bisa mengetahui bahwa ada 80 mahasiswa yang mengikuti ujian, nilai ujian terkecil adalah 35 dan tertinggi adalah 99. Nilai 70 merupakan nilai yang paling banyak diperoleh oleh mahasiswa, yaitu ada 4 orang, atau kita juga bisa mengatakan ada 4 mahasiswa yang memperoleh nilai 70, tidak ada satu pun mahasiswa yang mendapatkan nilai 36, atau hanya satu orang mahasiswa yang mendapatkan nilai 35.

Tabel 2b.



Tabel 2b merupakan daftar distribusi frekuensi dari data yang sudah dikelompokkan. Daftar ini merupakan daftar frekuensi yang sering digunakan. Kita sering kali mengelompokkan data contoh ke dalam selang-selang tertentu agar memperoleh gambaran yang lebih baik mengenai karakteristik dari data. Dari daftar tersebut, kita bisa mengetahui bahwa mahasiswa yang mengikuti ujian ada 80, selang kelas nilai yang paling banyak diperoleh oleh mahasiswa adalah sekitar 71 sampai 80, yaitu ada 24 orang, dan seterusnya. Hanya saja perlu diingat bahwa dengan cara ini kita bisa kehilangan identitas dari data aslinya. Sebagai contoh, kita bisa mengetahui bahwa ada 2 orang yang mendapatkan nilai antara 31 sampai 40. Meskipun demikian, kita tidak akan tahu dengan persis, berapa nilai sebenarnya dari 2 orang mahasiswa tersebut, apakah 31 apakah 32 atau 36 dst.

Ada beberapa istilah yang harus dipahami terlebih dahulu dalam menyusun tabel distribusi frekuensi.

Tabel 3.



Range : Selisih antara nilai tertinggi dan terendah. Pada contoh ujian di atas, Range = 99 – 35 = 64

Batas bawah kelas: Nilai terkecil yang berada pada setiap kelas. (Contoh: Pada Tabel 3 di atas, batas bawah kelasnya adalah 31, 41, 51, 61, …, 91)

Batas atas kelas: Nilai terbesar yang berada pada setiap kelas. (Contoh: Pada Tabel 3 di atas, batas bawah kelasnya adalah 40, 50, 60, …, 100)

Batas kelas (Class boundary): Nilai yang digunakan untuk memisahkan antar kelas, tapi tanpa adanya jarak antara batas atas kelas dengan batas bawah kelas berikutnya. Contoh: Pada kelas ke-1, batas kelas terkecilnya yaitu 30.5 dan terbesar 40.5. Pada kelas ke-2, batas kelasnya yaitu 40.5 dan 50.5. Nilai pada batas atas kelas ke-1 (40.5) sama dengan dan merupakan nilai batas bawah bagi kelas ke-2 (40.5). Batas kelas selalu dinyatakan dengan jumlah digit satu desimal lebih banyak daripada data pengamatan asalnya. Hal ini dilakukan untuk menjamin tidak ada nilai pengamatan yang jatuh tepat pada batas kelasnya, sehingga menghindarkan keraguan pada kelas mana data tersebut harus ditempatkan. Contoh: bila batas kelas di buat seperti ini:

Kelas ke-1 : 30 – 40

Kelas ke-2 : 40 – 50

:

dst.

Apabila ada nilai ujian dengan angka 40, apakah harus ditempatkan pada kelas-1 ataukah kelas ke-2?

Panjang/lebar kelas (selang kelas): Selisih antara dua nilai batas bawah kelas yang berurutan atau selisih antara dua nilai batas atas kelas yang berurutan atau selisih antara nilai terbesar dan terkecil batas kelas bagi kelas yang bersangkutan. Biasanya lebar kelas tersebut memiliki lebar yang sama. Contoh:

lebar kelas = 41 – 31 = 10 (selisih antara 2 batas bawah kelas yang berurutan) atau

lebar kelas = 50 – 40 = 10 (selisih antara 2 batas atas kelas yang berurutan) atau

lebar kelas = 40.5 – 30.5 = 10. (selisih antara nilai terbesar dan terkecil batas kelas pada kelas ke-1)

Nilai tengah kelas: Nilai kelas merupakan nilai tengah dari kelas yang bersangkutan yang diperoleh dengan formula berikut: ½ (batas atas kelas+batas bawah kelas). Nilai ini yang dijadikan pewakil dari selang kelas tertentu untuk perhitungan analisis statistik selanjutnya. Contoh: Nilai kelas ke-1 adalah ½(31+40) = 35.5

Banyak kelas: Sudah jelas! Pada tabel ada 7 kelas.

 

Frekuensi kelas: Banyaknya kejadian (nilai) yang muncul pada selang kelas tertentu. Contoh, pada kelas ke-1, frekuensinya = 2. Nilai frekuensi = 2 karena pada selang antara 30.5 – 40.5, hanya ada 2 angka yang muncul, yaitu nilai ujian 31 dan 38.

Vuln!! Path it now!!

wednesday,24 juli 2019

OLAH DATA STATISTIK
Uji Hipotesis

Dalam mempelajari karakteristik suatu populasi, seringkali kita telah memiliki hipotesis tertentu.  Sebagai contoh, pemberian DHA pada anak-anak akan menambah kecerdasannya atau  pemberian vaksin polio akan mengurangi jumlah anak-anak yang menderita penyakit ini.

Tentunya, setelah data diperoleh, gambaran yang diinginkan dari data tidak lagi hanya sekedar bagaimana karakteristik umum populasi tersebut (melalui pendugaan), namun lebih jauh yaitu apakah data mendukung hipotesis sebelumnya ataukah tidak (inferensia).

Dalam statistika, hipotesa mengenai populasi yang akan kita terima kebenarannya sampai ada bukti untuk menolaknya dinamakan sebagai hipotesis nol (null hypothesis/H₀). Apabila hipotesis ini ditolak kebenarannya, maka ada hipotesis lain yang kita anggap benar, yaitu hipotesis tandingan (Alternative Hypothesis/H₁).  Dalam perumusan H₁ dikenal dua macam hipotesis, yaitu:

a.Hipotesis Eka Arah

H₀:       m £ m₀                          H₀:       m ≥ m₀

H₁:       m ≥ m₀                          H₁:       m £ m₀

b.HIpotesis Dwi Arah

H₀:       m = m₀

H₁:       m ± m₀

Kesimpulan yang diperoleh dari uji hipotesis ini akan berkaitan dengan populasi, sedangkan penolakan atau penerimaan hipotesis didasarkan pada data contoh.  Sehingga akan muncul ketidakpastian.



Jenis Galat:

Galat Jenis I = penolakan H₀ yang benar

Galat Jenis II = penerimaan H₀ yang salah

a=P(galat jenis I)=peluang melakukan galat jenis I

b=P(galat jenis II)=peluang melakukan galat jenis II

Sifat-sifat :

• Jika a meningkat maka b menurun, dan sebaliknya.


• Jika ukuran sampel (n) meningkat maka nilai a dan b menurun, dan sebaliknya.

Uji Hipotesis Nilai Tengah Satu Populasi

Perumusan hipotesis nilai tengah satu populasi telah dikemukakan di awal.

à Untuk menolak atau menerima H₀ diperlukan informasi mengenai besarnya selisih antara xbar dengan mu pada H₀.



à Nilai selisih saja tidak cukup, karena tergantung satuan pengukuran peubah

à Kesalahan menebak 1.000.000 pada harga suatu mobil lain akibatnya pada harga komputer PC.

à Pengkoreksian berupa pembagian dengan simpangan baku dari xbar.

1. pembagian tersebut menghilangkan satuan pengukuran à ukuran relatif


2. mengakomodasi keragaman data

à Didapatkan kriterium (statistik uji) untuk mengevaluasi hipotesis, yaitu:



à Untuk

1. H₀:       m £ m₀

H₁:       m ≥ m₀

H₀ ditolak apabila Zhit > Za atau thit > t _{(db=n-1; a)}

1. H₀:       m ≥ m₀

H₁:       m £ m₀

H₀ ditolak apabila Zhit < Za atau thit < t _{(db=n-1; a)}

1. H₀:       m = m₀

H₁:       m ± m₀

H₀ ditolak apabila |Zhit| < Za/2 atau thit < t _{(db=n-1; a/2)}

Ilustrasi

Produk air minum dalam kemasan merk tertentu dengan kemasan gelas dicantumkan berisi air dengan volume 220 mL.  Produk ini akan dianggap baik apabila volume airnya tidak lebih atau kurang dari 220 mL.  Dari pemeriksaan terhadap 50 contoh produk ini didapatkan rata-rata volume airnya 218 mL.  Diketahui volume air produk tersebut menyebar normal dengan simpangan baku sebesar 2.5 mL.

Kesimpulan apa yang akan diambil apabila a=1%?

Uji Hipotesis proporsi satu populasi

à Perumusan Hipotesis:

1. Hipotesis Eka Arah

H₀:       p £ p₀                           H₀:       p ≥ p₀

H₁:       p ≥ p₀                           H₁:       p £ p₀

1. Hipotesis Dwi Arah

H₀:       p = p₀

H₁:       p ± p₀

à Kriterium (statistik uji) untuk uji proporsi:



à Untuk

1. H₀:       p £ p₀

H₁:       p ≥ p₀

H₀ ditolak apabila Zhit > Za atau thit > t _{(db=n-1; a)}

1. H₀:       p ≥ p₀

H₁:       p £ p₀

H₀ ditolak apabila Zhit < Za atau thit < t _{(db=n-1; a)}

1. H₀:       p = p₀

H₁:       p ± p₀

H₀ ditolak apabila |Zhit| < Za/2 atau thit < t _{(db=n-1; a/2)}

 

 

wednesday,24 juli 2019

OLAH DATA STATISTIK
Untuk membandingkan nilai tengah populasi dengan nilai tertentu antau dengan nilai tengah populasi lainnya bisa dilakukan dengan uji z. Namun uji z hanya bisa digunakan apabila data berdistribusi normal serta ragam populasi diketahui. Pada kenyataannya, jarang sekali kita bisa mengetahui nilai parameter suatu populasi dengan pasti, sehingga kita hanya bisa menduga parameter populasi tersebut dari sampel yang kita ambil. Karena kita tidak mengetahui berapa simpangan baku populasi, σ, maka nilai ini ditaksir dengan simpangan baku sampel, s, yang dihitung dari sampel. Hanya saja, untuk sampel berukuran kecil, s bukanlah nilai taksiran yang akurat untuk σ sehingga tidak valid lagi apabila kita menggunakannya untuk uji z. Untuk ukuran sampel yang kecil, kita bisa mendekatinya dengan menggunakan uji t-student.

Contoh

Uji t untuk 1 sampel

Hipotesis:

H0: µ_A = X

H1: µ_A ≠ X

Berdasarkan pengalaman pada tahun-tahun sebelumnya, suhu tubuh rata-rata mahasiswakedokteran yang baru masuk diyakini sebesar 98.6°F. Untuk memastikan bawa suhu tubuh rata-rata mahasiswa yang baru masuk tetap masih di bawah nilai tersebut, seorang mahasiswa senior berencana akan mengecek kembali klaim tersebut. Namun karena kesibukannya, dia hanya mengumpulkan data dari 12 mahasiswa. Rata-rata suhu tubuh ke-12 mahasiswa tersebut adalah sebagai berikut:
98.0       97.5        98.6        98.8        98.0        98.5        98.6        99.4        98.4        98.7        98.6

97.6

Untuk menguji klaim tersebut, dia menggunakan taraf nyata 0.05 yang menyatakan bahwa rata-rata suhu tubuh memang berasal dari populasi mahasiswa dengan rata-rata kurang dari 98.6°F.

Dengan menggunakan SPSS

Klik Analize-Compare Means- One Sample T test



Masukan peubah Suhu ke Test Variabel, kemudian isi Test Value dengan 98.6



Output:

T-Test

One-Sample Statistics

One-Sample Test

Interpretasi:
nilai-p sebesar 0.205 > alpha 5%, tidak tolak H0, dari hasi uji statistik diatas, kita tidak bisa menyatakan bahwa suhu tubuh mahasiswa baru sebesar 98.6°F. Meskipun nilai rata-ratanya memang lebih kecil, namun dari 12 sampel yang diambil, tidak cukup kuat untuk menyatakan bahwa suhu tubuh mahasiswa sebesar 98.6°F.

Uji-t untuk 2 Sampel Bebas

Uji t 2 sampel bebas ditujukan untuk menguji apakah ada perbedaan nilai 2 sampel  yang diberi perlakuan yang berbeda. Tidak seperti pada sampel berpasangan, uji sampel bebas benar - benar menggunakan 2 sampe yang berbeda.

Contoh menggunakan SPSS

Analyze-compare means- independent sample T-test



Masukan Data ke test Variabel, kemudian masukan Kategori ke Grouping Variable, lalu OK



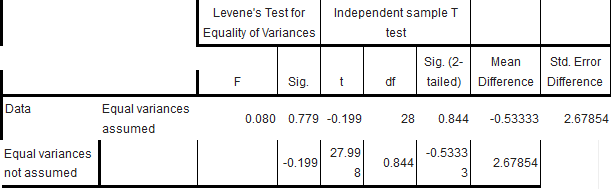
Output:

Group Statistics

Intrepretasi hasil uji t :
1. Bagian Group Statistics menggambarkan deskripsi masing-masing variabel.

2. Tabel ke dua Independent Sample Test menggambarkan hasil uji t berpasangan. Lihat kolom sig.(2 tailed). diperoleh nilai significancy 0,844(p>0,05), artinya "tidak ada perbedaan rerata stres karyawan yang berada pada ruang tradisional dengan berapa pada ruang modern".

OLAH DATA STATISTIK
Uji t berpasangan (paired t-test) adalah salah satu metode pengujian hipotesis dimana data yang digunakan tidak bebas yang dicirikan dengan adanya hubungan nilai pada setiap sampel yang sama (berpasangan). Ciri-ciri yang paling sering ditemui pada kasus yang berpasangan adalah satu individu (objek penelitian) dikenai 2 buah perlakuan yang berbeda. Walaupun menggunakan individu yang sama, peneliti tetap memperoleh 2 macam data sampel, yaitu data dari perlakuan pertama dan data dari perlakuan kedua. Perlakuan pertama mungkin saja berupa kontrol, yaitu tidak memberikan perlakuan sama sekali terhadap objek penelitian. Misal pada penelitian mengenai efektivitas suatu obat tertentu, perlakuan pertama, peneliti menerapkan kontrol, sedangkan pada perlakuan kedua, barulah objek penelitian dikenai suatu tindakan tertentu, misal pemberian obat. Dengan demikian, performance obat dapat diketahui dengan cara membandingkan kondisi objek penelitian sebelum dan sesudah diberikan obat.

Contoh menggunakan SPSS

H0: rata-rata sebelum sama dengan rata-rata sesudah

H1: rata-rata sebelum berbeda dengan rata-rata sesudah

Klik Analyze – Independent sample T test



Masukan data ke test variable(s), sampel ke grouping variable, kemudian klik Define Groups



Pada Groups 1 tulis T0 (sebelum), pada Groups 2 tulis T1 (sesudah), kemudian continue



Setelah itu klik OK, sampai keluar output



Nilai Sig.(2-tailed) sebesar 0.089 > alpha 5%, artinya tidak terdapat perbedaan antara data sebelum dengan data sesudah.